Ordinarily, one imposes the condition of self-adjointness on the Hamiltonian, representing the mathematical operation of complex conjugation and matrix transposition. This conventional Hermiticity condition is sufficient to ensure that the Hamiltonian H has a real spectrum. However, replacing this mathematical condition by the weaker and more physical requirement of combined parity reflection and time reversal PT, one obtains new classes of complex Hamiltonians whose spectra are still real and positive.

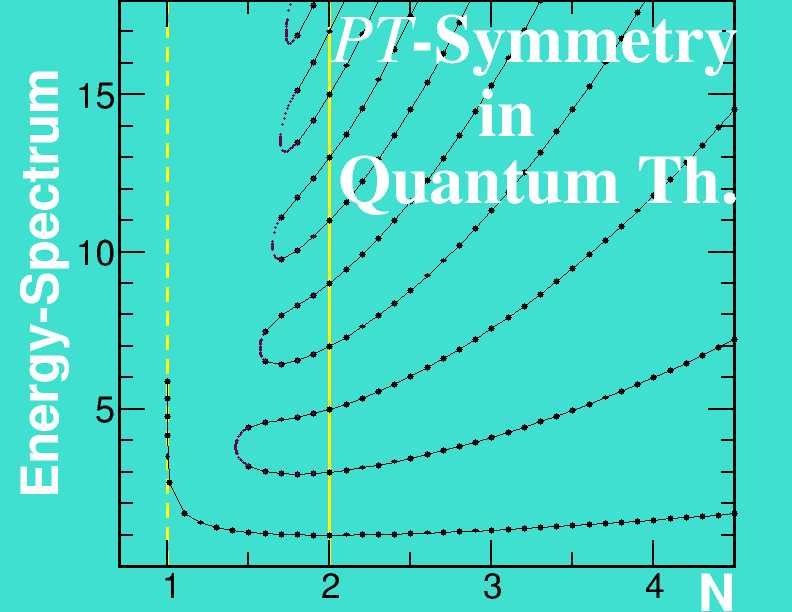
Together with Carl Bender and others, I have studied such generalization of Hermiticity using a complex deformation H=p²-(ix)^N of the harmonic oscillator Hamiltonian, where N is a real parameter. The system exhibits two phases: When N>=2, the energy spectrum of H is real and positive as a consequence of PT-symmetry. However, when 1< N<2, the spectrum contains an infinite number of complex eigenvalues and a finite number of real, positive eigenvalues because PT-symmetry is spontaneously broken. The phase transition that occurs at N=2 manifests itself in both the quantum-mechanical system and the underlying PT-symmetric classical system. This idea has captured the imagination of many researchers, with regular conferences dedicated to non-hermitian Hamiltonians.

Currently, we are studying applications of PT -symmetric theories in Quantum Field Theory, where they may provide generically parity broken physical models with real spectra.