Research on Networks and Random Walks:
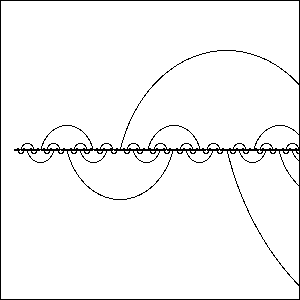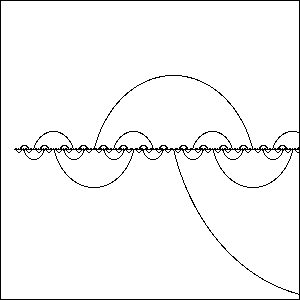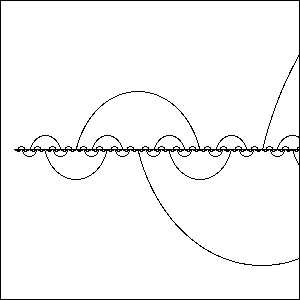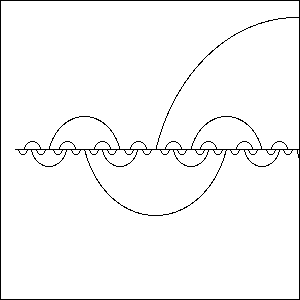
With B. Goncalves, I have introduced two new classes of networks that resemble small-world properties. These networks are recursively constructed but retain a fixed, regular degree. They consist of a one-dimensional lattice backbone overlayed by a hierarchical sequence of long-distance links. Both types of networks, one 3-regular and the other 4-regular, lead to distinct behaviors, as revealed by renormalization group studies. The 3-regular networks are planar, have a diameter growing as N1/2 with the system size N, and lead to super-diffusion with an exact, anomalous exponent, but possesses only a trivial fixed point Tc=0 for the Ising ferromagnet. In turn, the 4-regular networks are non-planar, have a diameter growing as ~2√[log N], exhibit "ballistic" diffusion (dw=1), and a non-trivial ferromagnetic transition, Tc>0. It suggest that the 3-regular networks are still quite "geometric", while the 4-regular networks qualify as true small-world networks with mean-field properties. Synchronization of processors on these networks is an example of an engineering application. |
We modeled diffusion on these networks by studying the mean-square displacement of random walks with time, < r2>~ t2/dw. It is found that diffusion -- the quintessential mode of transport throughout Nature -- proceeds faster than ordinary, in one case with an exact, anomalous exponent dw=2-log2(f)=1.30576.... It is an instance of a physical exponent containing the ``golden ratio'' f=(1+√5)/2 that is intimately related to Fibonacci sequences and since Euclid's time has been found to be fundamental throughout geometry, architecture, art, and Nature itself. It originates from a singular renormalization group fixed point with a subtle boundary layer, for whose resolution f is the main protagonist. The origin of this rare singularity is easily understood in terms of the physics of the process. Currently, we are studying a number of non-equilibrium processes on these networks, for which they may provide non-trivial but potentially solvable instances, such as self-avoiding walks, contact and exclusion processes, sandpile models, etc. |
|
Early on, in collaboration with Carl Bender, I have devised a new random walk model on a hyper-spherical lattice. With this model I can analytically investigate the behavior of dissipative systems and their interaction with boundaries in arbitrary dimensions. It provides an analytical continuation for a discrete random walk to non-integer dimensions by reducing the D-dimensional walk equation into a one-dimensional, radial difference equation with variable coefficients. The model permits the determination of the universal scaling near the polymer adsorption transition at hyper-spherical interfaces, such as a cell membrane. |
|
©1996-2002 Physics Department, Emory University. These pages may be freely distributed if unmodified. Last Update: 9/26/02; 2:55:53 PM For more information, contact: webmaster@physics.emory.edu |