Research on Spin Glasses:
| While theories for mean-field spin glass are well-developed, their applicability to finite-dimensional spin glasses is still in question. For many years, progress in verifying those theories using simulations have been hampered by the complexity inherent to the task: Just finding a ground state is an NP-hard problem, i.e. it is in the class of the most difficult computational problems known. This is a fruitful and pioneering research area at the interface of statistical physics and computer science, spawning interest in New Optimization Algorithms in Physics. While many areas of science are driven by rapidly improving hardware, the complexity of strongly disordered systems also requires the development of sophisticated methods and algorithms that may anticipate the fate of computational sciences beyond Moore's Law. |  |
|
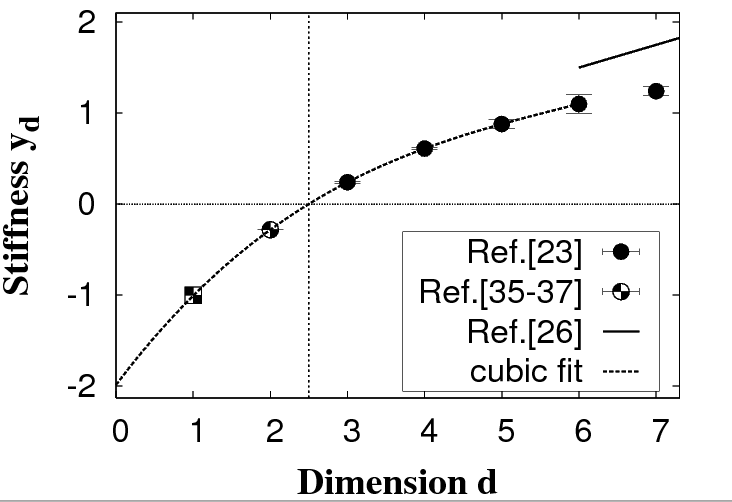
We have pioneered several new approaches to low temperature spin glasses, in particular, the Extremal Optimization (EO) heuristic (see DEMO here). By focusing on dilute lattices and effective data structures, we succeeded to improve the accuracy in quantifying low-energy excitations in 3-dimensional spin glasses by an order of magnitude. Similarly, these methods allowed us to obtain accurate values for the stiffness exponent in all dimensions d=3 to 7 for the Edwards-Anderson model. Our approach can be applied to any large-scale spin-glass network. We have tested the algorithm by determining the stiffness exponent, and ground state overlap, entropy, and energy with high accuracy for the d=3 and d=4 Migdal-Kadanoff lattice. Our studies on Bethe lattices and random graphs have provided high-accuracy verification of mean-field calculations and a number of new predictions. Even for the fully connected Sherrington-Kirkpatrick spin glass at T=0, EO provides some of the most precise predictions to date (see DEMO here). |
|
©1996-2002 Physics Department, Emory University. These pages may be freely distributed if unmodified. Last Update: 9/26/02; 2:55:53 PM For more information, contact: webmaster@physics.emory.edu |