IDL>plot, m(0,*), m(7,*), /xl, /yl, ps = circ(), xr = [1,500], /xs

Tutorial on 2D particle tracking
Tutorial on 3D particle tracking
IDL>plot, m(0,*), m(7,*), /xl, /yl, ps = circ(), xr = [1,500], /xs |

|
rotvec - this keyword allows you to specify the inital orientation vector [by default, this vector is (1,0,0)]. For example, if you want to calculate the MSAD of vector (1,1,1), you call "m = rotmsd(RR, rotvec=[1,1,1])". You don't need to normalize this vector; the program will do it for you. This is especially useful when you're interested in computing how specific particles within a cluster rotate about the center of mass. Click here for an example of how to compute the motions of each particle within a cluster.
getvec - specifying this keyword overrides computing the MSAD. Instead, the program will return the trajectory of the orientation vector through space. So, if for example you wanted the trajectory of vector (1,1,1) through space, you use "vec = rotmsd(RR, /getvec, rotvec=[1,1,1])"
gettheta - specifying this keyword overrides computing the MSAD. Instead, the program will return trajectory of the orientation vector through a type of rotation space. Basically, a coordinate (θx,θy,θz) in the rotation space describes the cumulative rotations about specific axes. I.e., θx is the total amount that the orientation vector has rotated about the x-axis. To do this, call "theta = rotmsd(RR, /gettheta)". See References [1,2] at the bottom of the page for more details on the idea behind the rotation space.
The other allowed keywords are "maxtime", "quiet", "noplot", and "mydts", which have the same meaning as in "msd.pro".
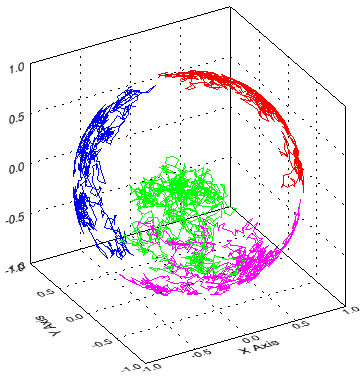
xplot3d, t0(0,*), t0(1,*), t0(2,*), xr=[-1,1], yr=[-1,1], zr=[-1,1]xplot3d, t1(0,*), t1(1,*), t1(2,*), /over, color=[0,1,0]*255xplot3d, t2(0,*), t2(1,*), t2(2,*), /over, color=[0,0,1]*255xplot3d, t3(0,*), t3(1,*), t3(2,*), /over, color=[1,0,1]*255 |
|
subroutines: