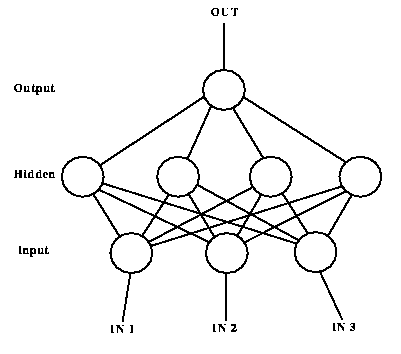
A neural network is a biologically-motivated computational construct. A network may be hardware or software based, and consists of several nodes, or neurons, connected by weighted communication lines. A neural network is a structure whose ith neuron has input value x_i, output value y_i = g(x_i) and connections to other neurons described by weights w_ij. The envelope function g(x_i) is commonly a sigmoidal function, g(x) = 1/(1+e^x). The input value x_i of neuron i is given by the formula x_i=Sum(j != i) w_ij y_j.
We use a feed-forward network, in which the neurons are organized into layers: an input layer, hidden layer(s), and an output layer. The input layer input values are set by the environment, while the output layer output values are returned to the environment (see figure below). The output information may be interpreted as a control signal, for example. The hidden layers have no external connections: they only have connections with other layers in the network. In a feed-forward network, a weight w_ij is only nonzero if neuron i is in one layer and neuron j is in the previous layer. This ensures that information flows forward through the network, from the input layer to the hidden layer(s) to the output layer. More complicated forms for neural networks exist and can be found in standard textbooks. Training a neural network involves determining the weights w_ij such that an input layer presented with information results in the output layer having a correct response. This training is the fundamental concern when attempting to construct a useful network.

We use neural networks to try to control chaos. Click here for more information. If you have any questions or comments, contact Eric at erweeks / emory.edu (replace the / with @).