Theorists like spin glasses
A spin glass is another glassy system that is frequently studied, often from a theoretical or computational point of view. Immagine a collection of spins (or compass needles) placed on a regular lattice. Here the disorder necessary to glassy dynamics is not in the spatial structure but in the randomness of the interactions between spins. Spin glass models can vary substantially in their details but they always require a mix of ferro- and antiferromagnetic interactions between spins, with spin pairs preferring an aligned or anti-aligned orientation respectively. At high temperatures, the spins do not feel the constraint of the interaction with their neighbors as much and are free to flip. As the temperature is lowered, the thermal energy Ethermal = kBT cannot overcome the interaction between spins which becomes dominant.
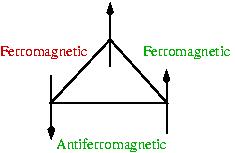 Crucial to the formation of a spin glass is the presence of frustration. As you can see in the figure on the right, a closed loop with an odd number of antiferromagnetic interactions cannot have all "bonds" satisfied (green). The unsatisfied bond (red) can be shifted around by flipping one of the spins but cannot ever be satisfied. Of course this frustration gets much worse when there are n spins that interact with each other through a distribution of bonds...
Crucial to the formation of a spin glass is the presence of frustration. As you can see in the figure on the right, a closed loop with an odd number of antiferromagnetic interactions cannot have all "bonds" satisfied (green). The unsatisfied bond (red) can be shifted around by flipping one of the spins but cannot ever be satisfied. Of course this frustration gets much worse when there are n spins that interact with each other through a distribution of bonds...
To learn more about spin glasses you can go and talk to Stefan Boettcher or visit his website.