Eric Weeks
- personal pages - research
- time series analysis
My Adventures in Chaotic Time Series Analysis |
weeks@physics.emory.edu |
Eric Weeks
- personal pages - research
- time series analysis
My Adventures in Chaotic Time Series Analysis |
weeks@physics.emory.edu |
A0. Links and related information
For an explanation of what these pages are all about, select topic 1 above.
This page: top | lorenz | rossler | henon | expt: periodic | qperiodic-2 | qperiodic-3 | chaotic | bottom
![]()
On this page, I have plotted the "attractors" for the seven time series. For the Lorenz attractor, I have shown what different choices for the delay will produce. For an explanation about delay coordinates, see the previous page.
There are six different versions of the Lorenz attractor shown below. The first is for a tiny delay (T=0.02), showing that the data lies very close to the line X(t)=X(t+T). The second is for the first minimum of the mutual information curve (T=0.16); this is the "best" attractor in the sense that the attractor occupies a large region of space. The third graph is T=0.22, the first maximum of the mutual information. This results in large portions of the attractor lying on top of each other (upper right and lower left of the graph). The fourth choice (T=0.40) is midway to the next local minimum in mutual information (T=0.62) which is the fifth graph. The last graph corresponds to the second local maximum in mutual information, T=0.74. The difference between the fifth and sixth graphs again is seen in the spreading out of trajectories in the fifth graph, compared with the bunching seen in the sixth graph.
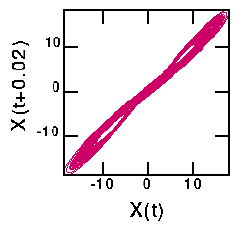
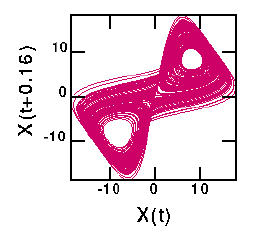
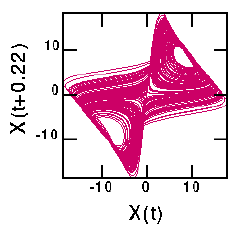
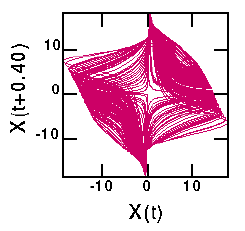
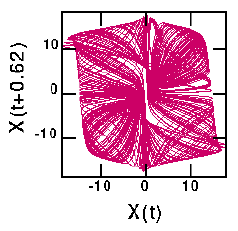
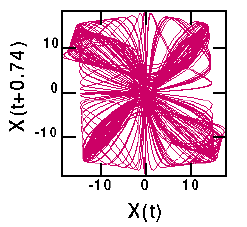
Reminder: the second graph above is the "best". Also, the original Lorenz equations are three-dimensional, so the attractor properly should be displayed in three dimensions. I actually recall that the fractal dimension of this attractor is close to 2, thus it looks reasonably nice when plotted in two dimensions.
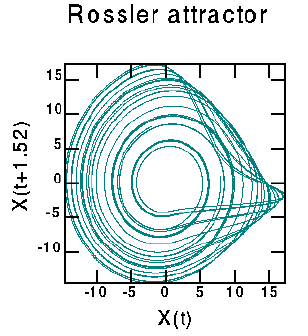
Recall that the equation describing the Rössler attractor are 3-dimensional.
This page:
top |
lorenz |
rossler |
henon |
expt: periodic |
qperiodic-2 |
qperiodic-3 |
chaotic |
bottom
Hénon:
time series
|
power spectrum
|
mutual information
|
attractor
|
attractor 3D
|
autocorrelation
|
poincare
|
1-D maps
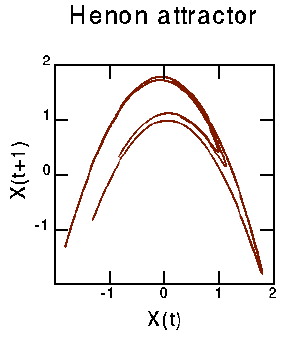
If you zoom in on portions of this attractor, you can see a fractal structure, although I have no illustrations of this right now. As the map is a 2-D map, the full structure of the Hénon attractor can be seen above; it does not need to be displayed in 3-D.
This page:
top |
lorenz |
rossler |
henon |
expt: periodic |
qperiodic-2 |
qperiodic-3 |
chaotic |
bottom
Experimental/periodic:
time series
|
power spectrum
|
mutual information
|
attractor
|
attractor 3D
|
autocorrelation
|
poincare
|
1-D maps
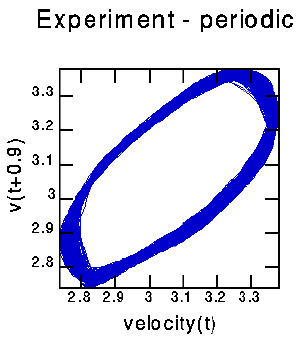
The graph shows a nice limit cycle, demonstrating that this is indeed periodic data. The thickness of the curve is related to the noise in the experiment, as well as the finite sampling of the data.
This page:
top |
lorenz |
rossler |
henon |
expt: periodic |
qperiodic-2 |
qperiodic-3 |
chaotic |
bottom
Experimental/quasiperiodic-2:
time series
|
power spectrum
|
mutual information
|
attractor
|
attractor 3D
|
autocorrelation
|
poincare
|
1-D maps
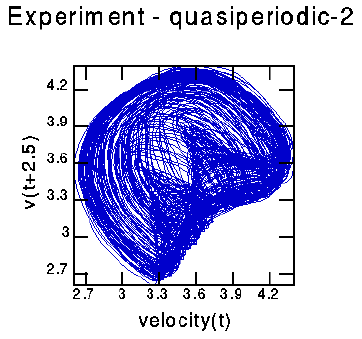
This is messier than the periodic case; the attractor properly lies in 3-dimensional space.
This page:
top |
lorenz |
rossler |
henon |
expt: periodic |
qperiodic-2 |
qperiodic-3 |
chaotic |
bottom
Experimental/quasiperiodic-3:
time series
|
power spectrum
|
mutual information
|
attractor
|
attractor 3D
|
autocorrelation
|
poincare
|
1-D maps
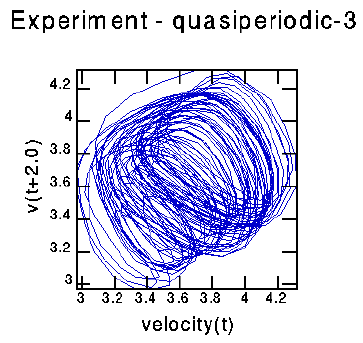
This is even messier than the quasiperiodic-2 case, as the attractor is best displayed in 4 dimensions. You'll have to download a special add-on to your web browser to display 4 dimensions properly.
This page:
top |
lorenz |
rossler |
henon |
expt: periodic |
qperiodic-2 |
qperiodic-3 |
chaotic |
bottom
Experimental/chaotic:
time series
|
power spectrum
|
mutual information
|
attractor
|
attractor 3D
|
autocorrelation
|
poincare
|
1-D maps
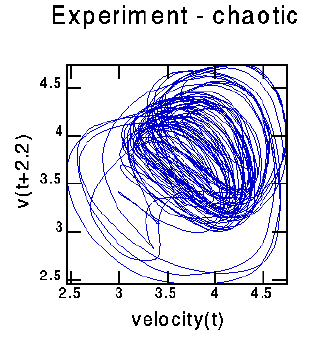
Again, somewhat messy, indicating that it's dimension is somewhat higher
than 2.
So far the analysis has given me several different times. From the Fourier transform I have certain characteristic periods. From the mutual information calculation I have the first minimum. Thus, a table:
Note that all times are in natural units (seconds for experimental data, iterations for Hénon map, the time step of the equations for the Rössler and Lorenz systems). Links in the table will take you to the appropriate location where the information was found.
![]()
 Previous page: Mutual information
Previous page: Mutual information
 Next page: Plotting these attractors in 3-D
Next page: Plotting these attractors in 3-D
This page: top | lorenz | rossler | henon | expt: periodic | qperiodic-2 | qperiodic-3 | chaotic | bottom
![]()