Eric Weeks
- personal pages - softwareSoftware for calculating mutual information from a time series |
weeks@physics.emory.edu |
Eric Weeks
- personal pages - softwareSoftware for calculating mutual information from a time series |
weeks@physics.emory.edu |
![]()
The method of "mutual information" is a way to determine useful delay
coordinates for plotting attractors.
Click here for more information on this method.
The method of mutual information for finding the delay T was proposed
in an article by
Andrew M. Fraser and
Harry L. Swinney ("Independent
coordinates for strange attractors from mutual information," Phys. Rev.
A 33 (1986) 1134-1140). I have written a program which carries out their
algorithm. If you would like to use Fraser's original software, check
his home page for the ftp link (his program is called "polly").
![]()
 Click here to download software.
To compile, use "cc -o minfo minfo5.c -lm".
Click here to download software.
To compile, use "cc -o minfo minfo5.c -lm".
To use the software, you can either specify the filename or pipe the data into the program:
or
There are three options. -h lists all the options with a brief comment to remind you what they do. -t (number) sets the maximum delay to calculate the mutual information for; the default is 20. The program calculates from 0 to the number you specify. -b (number) puts the data into 2^(number) equiprobable bins before doing the calculation; see below for discussion. Thus, to generate the graph below, I typed:
(and then rescaled the delay coordinate to be in terms of the period). The input data should be a list of numbers specifying the data (no times, just the data) and the output will be in the form (delay,information) with information given in bits.
If you have questions, please send me email; email address below.
![]()
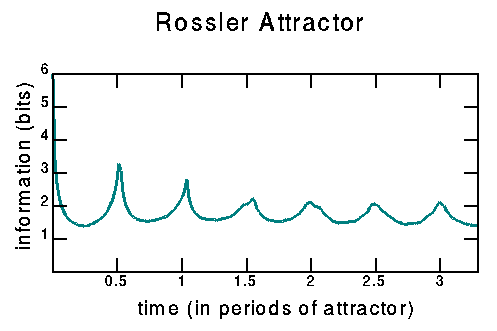
I verified that my program was working by duplicating their Fig. 2.
![]()
My program is actually slightly different from the algorithm Fraser and Swinney discuss. There are two differences:
1. I don't bother with their Eqs. 21 and 22. They use this algorithm to determine if there is substructure within a region. I exploit the fact that every 18 months computer power doubles, so that computer power has increased by roughly a factor of 200 since they wrote their article. Thus, rather than deciding whether there is substructure, and only investigating the substructure if it exists, I go ahead and just assume that there is substructure. In many cases this results in a faster program as I avoid calculating their check, and in the worst case you can depend on that factor of 200 in computer speed to keep the program running time down.
In practice, I get a speedup of roughly 50-100 over the times they quote in their article.
2. The second difference is that I use a somewhat crude method for binning the data. Their algorithm starts by placing data into equiprobable bins. This is useful as it reduces problems noise might cause, as well as speeding up the algorithm. My method for binning is to sort all of the data (as is needed for their algorithm) and then asserting that the first N data points are the same, the next N are the same, etc. Thus I am putting data into bins N wide. N must be a power of 2. The data in fact might not evenly divide into these bins, although in practice this seems not to matter much. As their method is intended to give guidance into a good delay to use for investigating strange attractors, the error my binning algorithm introduces ought to be extremely small. The agreement I get with the results of Fraser and Swinney convinces me that my program is performing well.
![]()
The graph was made with a program I wrote, psdraw. This program is public domain. The program makes PostScript output which I then converted to GIF.