Research on Extremal Optimization:
| As an important practical application resulting from my research on Self-Organized Criticality (SOC), Allon Percus and I have developed a powerful general-purpose method to approximate (NP-)hard optimization problems. The method is inspired by the far-from-equilibrium dynamics often found in nature where extremely bad adapted components of a system are selectively driven to extinction, leaving behind complex and highly adapted structures (such as eco-systems). This "Extremal Optimization" approach provides a new philosophy to optimization in its use of non-equilibrium statistical physics and in merely selecting against the bad instead of favoring the good. In this sense it complements other general-purpose methods such as "Simulated Annealing" or "Genetic Algorithms," both of which it can dominate computationally in quality, speed, and memory requirements. Mimicking the dynamics of slowly driven dissipative systems, it is free of tunable parameters such as temperature schedules or selection criteria. |
|
An optimization heuristic base on a non-equilibrium process such as EO appears to be capable to elucidate the properties of phase transitions in combinatorial optimization problems. We have demonstrated these properties so far for graph partitioning and the 3-coloring problem. EO has received grant support by Los Alamos and the NSF. There are also a number of studies on EO by other groups. A Wikipedia blog on EO has been started by J. Brownlee. EO has found a large number of applications by other |
Java Applet Demo: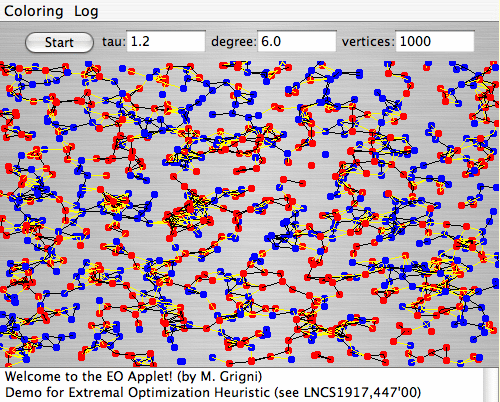
|
Most generally, "Extremal Optimization" operates on a "fitness"
defined for each variable in a system which takes the place
of the usual cost function. This fitness is a local measure of how
well each particular variable fits into a solution. In close
similarity to SOC models such as the Bak-Sneppen
model (DEMO), the algorithm proceeds as follows:
While the state of the system may fluctuate widely ("avalanching"), the bias against badly adapted elements of the solution pushes the system repeatedly in the neighborhood of near-optimal solutions. Only the best of those solutions will have to be remembered along the way and is returned at the end of a "run." |
| This algorithm applied to Graph Partitioning performs at least as well as Simulated Annealing. In particular, Extremal Optimization does well near critical points inherent to many NP-hard problems, where Simulated Annealing (and many other methods) fail. Such a heuristic is very useful in physics as a tool to explore the ground state properties disorder systems such as Spin Glasses. In particular, Extremal Optimization helped to confirm predictions for Mean-Field Spin Glasses obtained with Replica Symmetry Breaking (RSB) and to obtain the stiffness exponent y=0.24(1) governing thermal "droplet" excitations in the d=3 Edwards-Anderson model (EA). As a consequence, we were able to predict the lower critical dimension for EA to be d=5/2. More recently, we have shown that EO produces excellent results also for highly connected variables, such as in the Sherrington-Kirkpatrick model. | Java Applet Demo: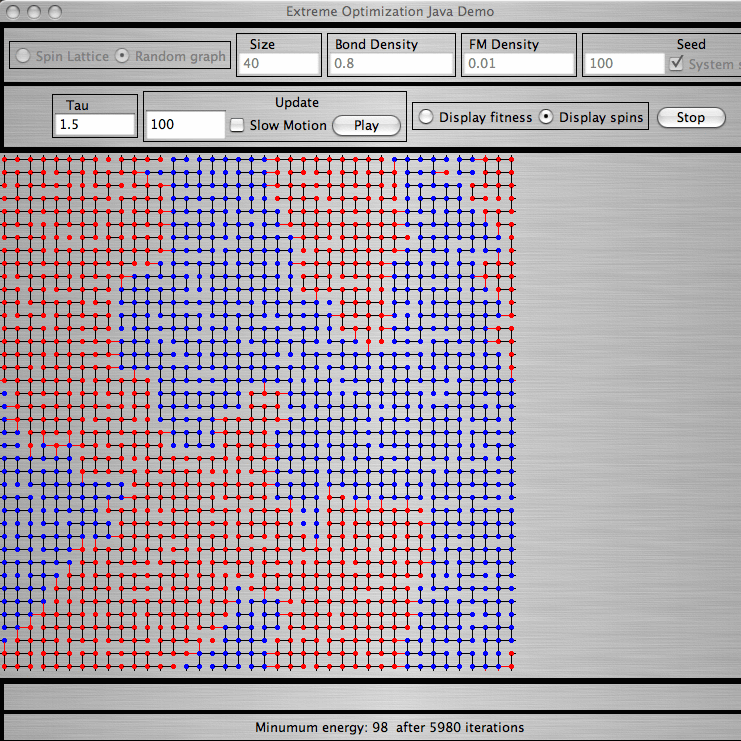
|
|
©1996-2002 Physics Department, Emory University. These pages may be freely distributed if unmodified. Last Update: 9/26/02; 2:55:53 PM For more information, contact: webmaster@physics.emory.edu |