Demos and Downloads:
Some coding-projects, finished or under development, can be found at our SourceForge Site.
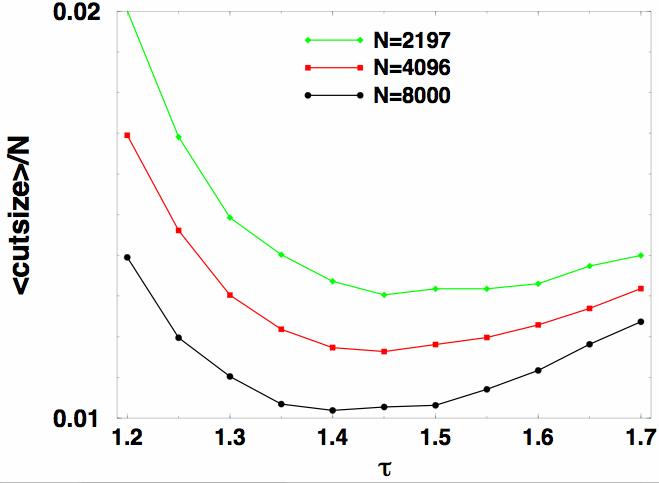
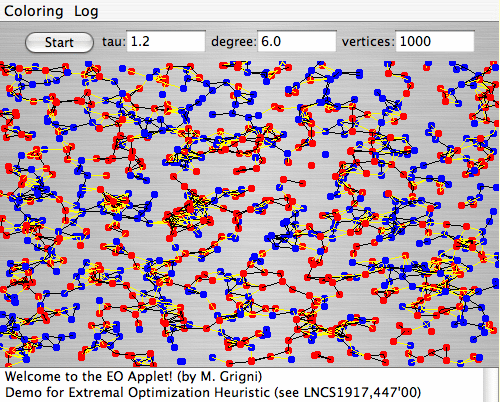
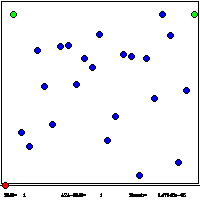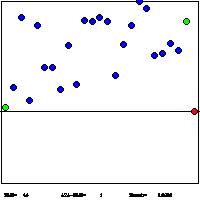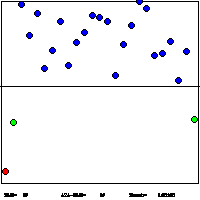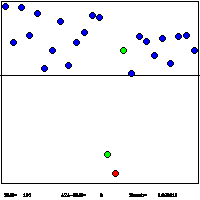
1. Extremal Optimization Demo for Graph Bi-Partitioning:This Java applet demonstrates the behavior of τ-EO. In this variant of EO, a variable is chosen for an update according to a scale-free power-law distribution over the fitness rank k [ie. P(k)∼k -τ]. When τ >>1, only the lowest-ranked ("worst") variable with k=1 is updated, as described here. Such a local search often is too greedy, with update-activity much to localized on a few variables. If τ→0, variables are updated randomly and nothing is learned (not good!). Optimal behavior is obtained at intermediate values of τ (see Figure), where τ-EO maintains a strong bias to select low-ranked fitnesses (small k), but enough scale-free (non-equilibrium) fluctuations are induced to escape local minima. GBP tries to partition the N vertices of a graph into two equal-sized (N/2) sets such that the number of edges between the two sets is minimal. Better heuristics than EO exist for this problem, based on the obvious clustering behavior of the vertices (see eg. METIS). Here, we don't even use clustering at start-up, using a random assignment instead, to get EO pure. |
Lowest cost solutions found, averaged over a number of instances and EO-runs, as a function of τ for various graph sizes N. An optimal choice for τ emerges, which scales like τ-1∼1/log(N). Larger τ are too greedy, smaller τ are too random. |
This applet was written by Mic Grigni: |
Some things to try:
|
This applet was written by Emiliano Marchetti:
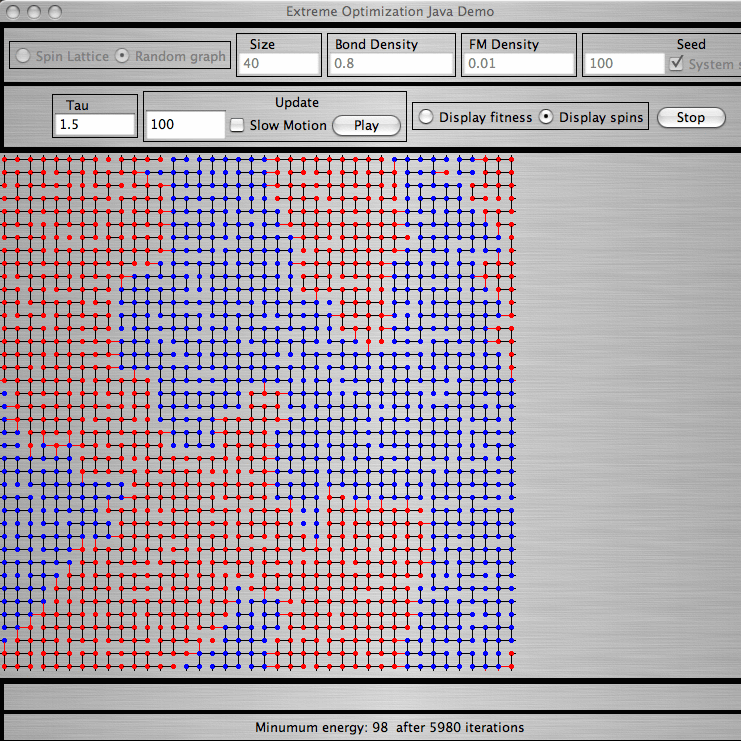 |
2. Extremal Optimization Demo for Spin Glasses:This Java applet also demonstrates the behavior of τ-EO, but for finding ground states of lattice spin glasses in d=2. (It also does Graph Partitioning for a dilute mesh; which corresponds to a bond-dilute ferromagnet fixed at zero magnetization!) The EO-algorithms is as described above. Again, there are much better, exact algorithms for this polynomial problem (see also the spin glass server in Köln), and EO distinguishes itself for spin glasses only for d >2. But problems in d >2 are harder to visualize. Some things to try:
|
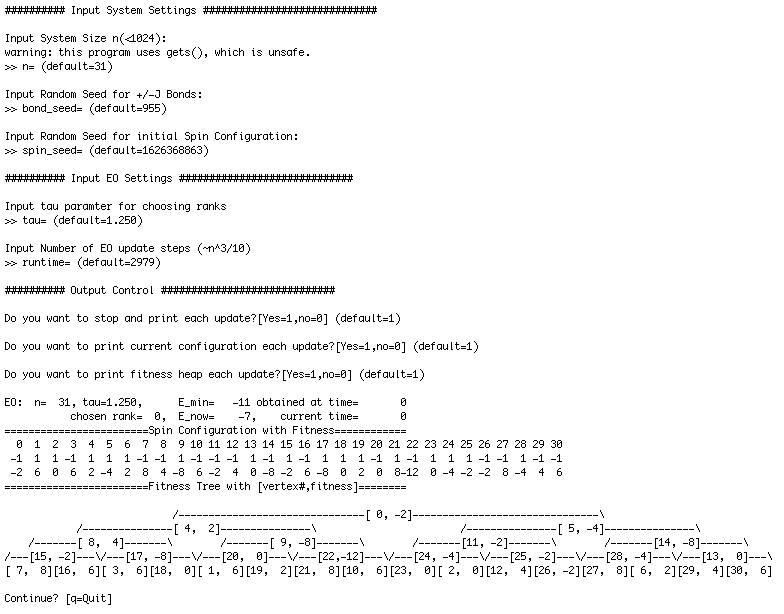
3. Extremal Optimization Demo for SK-Spin Glasses:This is a simple demo for the τ-EO algorithm described and used for the Sherrington-Kirkpatrick (SK) spin glass model. It's a monolithic C-program (last bug fix on 6/20/06) to download and compile with "gcc -O3 -lm demoSK.c -o demoSK.exe" or similar. Run "demoSK.exe" on any dumb terminal; it should be sufficiently clear (see Screenshot). The EO-algorithm uses (and displays) tree-ordered fitnesses, as first described here. Some things to try:
|
EO for SK Demo: |
4. Extremal Optimization Demo for 2d Spin Glass:This is a colorful demo of τ-EO on a 2d spin glass, similar to the above applet. Though, this is a monolithic C-program, eoglasspolt.c, for download and it requires the libraries in the "plotutils" package. (Works for me on Redhat/ Fedora, 'don't know about other platforms!) Compilation instructions are on first line of file. OK interface, but poorly documented. Displayed on the lattice are merely the fitnesses of spins (from black=good to red=bad), not their orientation! Colors fade the longer a spin remains untouched. Some things to try:
|
 |
5. Bak-Sneppen Demo:A simple program to demonstrate the Bak-Sneppen model of SOC, on which I have done some work. In particular, it has been the basis of the above Extremal Optimization (EO) heuristic. It consists of a lattice of uniform random numbers on [0,1] (=``fitnesses'' of species, say). Each time step, the smallest (``least fit'') number and its (``co-dependent'') neighbors are replace with new random numbers. A self-organized critical (SOC) state emerges with scale-free fluctuations and ``punctuated equilibrium''. As above, this is a monolithic C-program, baksneppen.c, for download and it requires the libraries in the "plotutils" package. (Works for me on Redhat/ Fedora, 'don't know about other platforms!) Compilation instructions are on first line of file. The implementation is most primitive, but the animation may be interesting. |
Funding:Our work on disordered systems is currently supported by a DMR grant from the NSF. Another grant from the NSF has supported our research on Extremal Optimization. Computational equipment was purchased through a grant from the Emory University Research Council (URC), and start-up support. Previous partial support for Extremal Optimization was received from an LDRD-funded project at Los Alamos National Laboratory. |
|
©1996-2002 Physics Department, Emory University. These pages may be freely distributed if unmodified. Last Update: 9/26/02; 2:55:53 PM For more information, contact: webmaster@physics.emory.edu |