Eric Weeks
- personal pages - miscSpiral TrianglesA simple way to make interesting spirals. See the bottom of the page for links to other simple algorithms like this one. |
weeks@physics.emory.edu |
Eric Weeks
- personal pages - miscSpiral TrianglesA simple way to make interesting spirals. See the bottom of the page for links to other simple algorithms like this one. |
weeks@physics.emory.edu |
 NOTE: I also wrote
a page about mathematical spirals (Archimedes' Spiral, etc).
NOTE: I also wrote
a page about mathematical spirals (Archimedes' Spiral, etc).
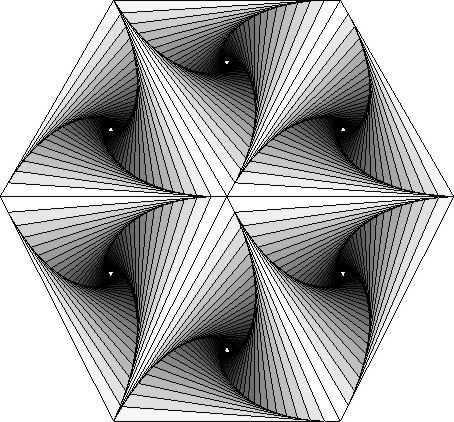
I learned this idea from George Francis when I took his Math 198 class (which, from his web page, it looks like he is still teaching; it's a good class, I recommend it).
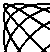
The basic idea is to start with a triangle, interpolate to find a point a fraction of the way down a side, draw a line to this point, and use that point as the new corner for the triangle. This will make a picture that looks like this:
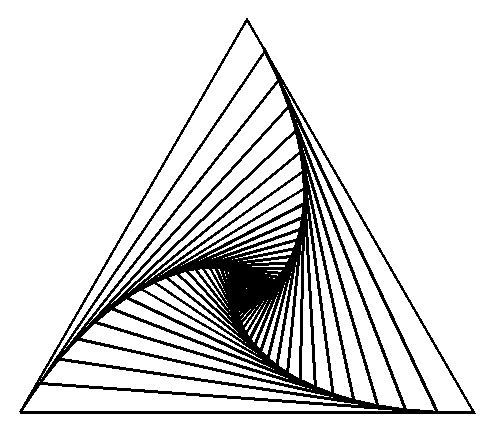
Here's the simple awk script that made that picture:
The variable "ee" is the scale factor used to determine how tight the spiral is.
The program psdraw is a utility I wrote to make simple postscript plots. Click here for more information on psdraw.
Since psdraw can handle colors, I could make the following picture:

That was made with this script (using "gawk" to handle trig functions):
Of course, if you write a computer program you can do some more powerful things (such as the picture at the top of the page). I just put in the awk scripts to emphasize how simple this algorithm is. I wrote a C program that fills the triangles, and makes six in a pattern. This program made the picture at the top, and made the following pictures:
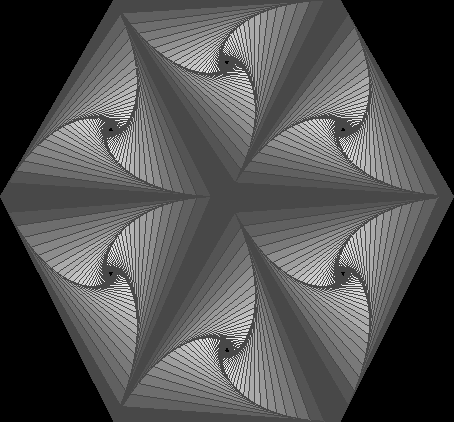

 Click here to get a copy of this C program. To compile, use
"cc -o spiral spiral.c -lm".
Click here to get a copy of this C program. To compile, use
"cc -o spiral spiral.c -lm".
 NOTE: I just added
a page about mathematical spirals (Archimedes' Spiral, etc).
NOTE: I just added
a page about mathematical spirals (Archimedes' Spiral, etc).
Hey, someone linked to this web page! There is a French web page with lots of math resources that put in a link to this page.
Click here to learn how to convert PostScript pictures to GIF.
![]()




This page created August 27, 1996.